Obwohl ich schon ein quadratisches Zelt habe, hat mir die Kostruktion einiges Kopfzerbrechen bereitet.
Von Anfang an war klar, daß die Seitenlänge ca. 3 Meter betragen sollte, und daß die Seiten zusätzliche Steher (d.h. senkrechte, abgespannte Stangen) brauchen. Das alte Zelt hat an der Dachkante eine Seitenlänge von 2,4 m und hängt selbst bei stammster Abspannung ein wenig durch. Da das Bett an einer Wand stehen muß, hing die Seite immer ein wenig über das Bett, was vor allem in Regennächten kein schönes Gefühl ist.
Es war auch abgemacht, daß die Wände extra Teile werden sollten, um mittels Haken und Ösen ans Dach gehängt zu werden, wie es auch bei den Militärzelten der Fall war. Beim alten Zelt sind Dach und Wände zu einem Teil zusammengenäht, aber da Leinen viel schwerer ist als Baumwolle, kam das nicht in Frage. Außerdem wollte ich unbedingt Fenster mit Raffrollos haben (auch die gab es bei den Militärzelten!), denn selbst bei mäßig warmem Wetter kann sich in einem Zelt unglaubliche Hitze stauen.
Die Wände sollten möglichst wieder 1,8 m hoch sein, damit man sich beim eintreten nicht bücken muß. Das wären dann (bei einer Seitenlänge von 3 m) 12 x 1,8 Meter. Deshalb sollten die Wände aus mindestens zwei Teilen bestehen, damit ich nicht so viel Stoff auf einmal schleppen muß. Die Möglichkeit, eine Seite als Sonnensegel hochzuklappen, hätte ich gern behalten, aber das hätte eine Dreiteilung der Wände bedeutet: 3 Meter Sonnensegel plus 9 Meter, die zu halbieren wären. Das war symmetrisch nicht zu machen, weil noch zwei weitere Überlegungen ins Spiel kommen:
Daß man im 18. Jh. aus technischen Gründen selten breiter als 1 m gewebt hat (d.h. ein authentisches Zelt darf keine breiteren Bahnen haben) und daß Bahnen von 1 m Breite gut auf die verfügbaren Stoffballen (Breite 2,15 m) paßten. Für Bahnen von 1 m Breite sprach auch, daß ich auf diese Weise zwei Steher pro Seite anbringen konnte: Bei den historischen Zelten sind Steher immer da angebracht, wo auch eine Naht im Zeltstoff ist, die zusätzlich mit einem Leinenband verstärkt ist. Das hat sicherlich statische Gründe. Ich hätte die 9 Meter also 4:5 aufteilen müssen, was mich per se nicht gestört hätte, aber der asymmetrisch versetzte Hintereingang hätte nicht dazu gepaßt, wie ich die Inneneinrichtung verteilen mußte.
Ich entschied mich daher für eine Lösung ohne Sonnensegel (mittlerweile habe ich sowieso ein extra-Segel), die der Konstruktion der ovalen Militärzelte ähnelt: In der vorderen und hinteren Mitte ist jeweils eine Bahn am Zeltdach angenäht, die den vorderen und hinteren Eingang darstellt; beidseits davon werden dann die beiden Wandteile (je 5 x 1,8 m) ans Dach gehakt. In die Mitte derselben, d.h. in die Mitte beider Seitenwände, kommen dann die beiden Fenster.
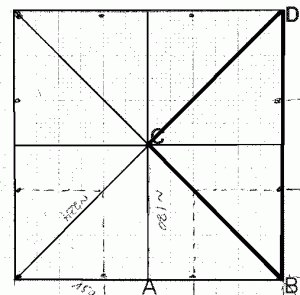
Das Dach stellte eine rechte Herausforderung dar. Es besteht aus vier gleichschenkligen Dreiecken (eins pro Seite des Quadrats, im Bild unten CBD), die wiederum als je zwei rechtwinklige Dreiecke (ABC) aufgefaßt werden können:
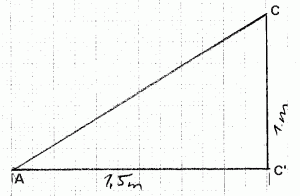
Da alle acht rechtwinklige Dreiecke sind, müßte sich die Länge der Schräge (d.h. der Strecke zwischen Eckpfosten B und Mittelpfosten C) nach Pythagoras berechnen lassen, wenn die Längen der anderen zwei Seiten ([AB] und [AC]) bekannt sind. Die Länge der unteren Kante [AB] ist klar: halbe Seitenlänge, also 1,5 Meter. Und die Höhe? Bei meinem alten Zelt ist die Mittelstange 1 m höher als die Wände, aber da das Dach schräg ist, beträgt die Höhe der Stoffbahn eben nicht 1 m. Um zu bestimmen, wie hoch so ein achtel-Dreieck sein soll, muß man das Zelt von der Seite her betrachten:
Das ist wieder ein rechtwinkliges Dreieck. Laut Pythagoras ist a²+b²=c², oder [AC‘]²+[CC‘]²=[AC]², oder 1,5²+1²=[AC]², oder 2,25+1=?[AC] ? 1,8. Die Seite [AC] ist also etwa 1,8 m lang. Nach dem gleichen Schema können wir nun die Schräge [BC] berechnen: [AB]²+[AC]²=[BC]² oder 1,5² + 1,8² = [AC]² oder 2,25 + 3,24= ?[AC] , d.h. [AC] ? 2,34.
Um meinen Plan zu überprüfen, baute ich ein Modell aus Papier. Die Maße stimmten, aber die Dachschräge stellte sich als zu flach heraus (was auch logisch ist, da das neue Zelt ja etwas größer ist als das alte): Je steiler die Dachneigung, desto besser läuft der Regen ab, desto weniger leicht suppt es durch. Ich verlängerte also die Mittelstange auf 2,9 m – die zehn Zentimeter machen erstaunlich viel aus – und berechnete alles neu.
Da die Bahnen nur 1 m breit sein sollen, und weil es sinnvoll ist, die Steher da anzubringen, wo eine Naht den Zeltstoff verstärkt, sollten auch die Dach-Bahnen einen Meter breit sein. Das bedeutet, daß es eine mittlere Bahn gibt, die entlang der Mitte ca. 2,4 m lang ist und 1 m breit, und seitlich daran angesetzt je zwei rechtwinklige Dreiecke, die jeweils ebenfalls 1 m breit sind.
Nun erst konnte ich den Stoffverbrauch bestimmen. Schon im Vorfeld hatte ich festgestellt, daß die günstigste Quelle für Leinwand der Künstlerbedarfshandel Boesner ist. Für die Wände hatte ich schon früher einen Ballen (10m x 2,15 m) der Sorte Toledo besorgt. Toledo ist ein mittelschweres (375g/m²), relativ günstiges (ca. 180 € pro Ballen) Leinen, das nicht allzu dicht gewebt ist und daher nicht für ein Zeltdach geeignet. Aber für senkrechte Wände, so dachte ich mir, müßte es reichen, zumal die Wände gefüttert werden sollen – was sie noch schwerer macht, so daß es erst recht sinnvoll ist, einen leichteren Stoff zu wählen. Ein Ballen reicht für meine Zwecke um 2 m nicht, aber ich hatte früher schon einen halben Ballen Toledo sehr günstig auf eBay geschossen. Fürs Dach hatte ich die Sorte Toscana (ebenfalls von Boesner, ebenfalls 10 m x 2,15 m) vorgesehen, die viel dichter, aber auch viel schwerer ist (510g/m²). Das Dach wollte ich nicht füttern, um es nicht noch schwerer zu machen (nach meinenr Rechnung wird es schon ohne die angesetzten „Türen“ ca. 12 kg wiegen), außerdem hätte der Futterstoff nicht ausgereicht. Als Futter hatte ich 17 Meter eines IKEA-Stoffs mit 18.-Jh.-Muster gekauft – einen der letzen, bevor auf allzu moderne Muster umgestellt wurde – , ohne genau zu wissen, wieviel ich brauchen würde. Es sieht so aus, als ob es knapp werden würde. Da der Futterstoff eine Bahnbreite von 1,5 m hat, die Außenhülle aber eine von 1 m, wird das Futter in der Mitte einiger Zeltbahnen eine Naht haben müssen.